Valor absoluto
En matemática, el valor
absoluto o módulo1 de un número real es
su valor numérico sin
tener en cuenta su signo,
sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y
de -3.
El valor absoluto está relacionado con las
nociones de magnitud, distancia y norma en
diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un
número real puede generalizarse a muchos otros objetos matemáticos, como son
los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
Valor absoluto de un número complejo[editar]
Como los números complejos no conforman un conjunto ordenado en el sentido de los reales, la generalización del concepto no es directa, sino que requiere de la siguiente identidad, que proporciona una definición alternativa y equivalente para el valor absoluto:
De esta manera, dado cualquier número complejo de la forma
con x e y números reales, el valor absoluto o módulo de z está definido formalmente por:
Como los números complejos son una generalización de los números reales, es lógico que podamos representar a estos últimos también de esta forma:
De modo similar a la interpretación geométrica del valor absoluto para los números reales, se desprende del Teorema de Pitágoras que el valor absoluto de un número complejo corresponde a la distancia en el plano complejo de ese número hasta elorigen, y más en general, que el valor absoluto de la diferencia de dos números complejos es igual a la distancia entre ellos.
ejemplos




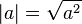

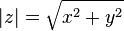

No hay comentarios.:
Publicar un comentario