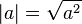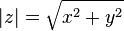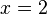raiz cuadrada

Raíz cuadrada

Notación matemática de raíz cuadrada de x.

En matemáticas, se llama raíz cuadrada de un número positivo a un segundo número positivo que al multiplicarlo por sí mismo resulta el valor del primero, es decir, que es un segundo número que al elevarlo al cuadrado es igual al primero. Abreviado como raíz tiene el símbolo: $\sqrt{\ }$ . Es la radicación de índice 2 o, equivalentemente, la potenciación con exponente ¹/₂.

El concepto de raíz cuadrada puede extenderse a cualquier anillo algebraico, así es posible definir la raíz cuadrada de un número negativo o la raíz cuadrada de algunas matrices. En los números cuaterniónicos los reales negativos admiten un número infinito de raíces cuadradas, sin embargo el resto de cuaterniones diferentes de cero admiten solo dos raíces cuadradas.

¿Como se resuelve la raíz cuadrada de un entero sin calculadora ?

Veamos un ejemplo

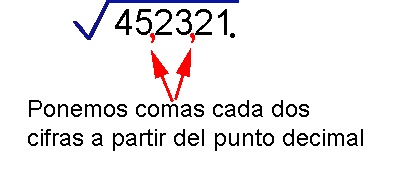
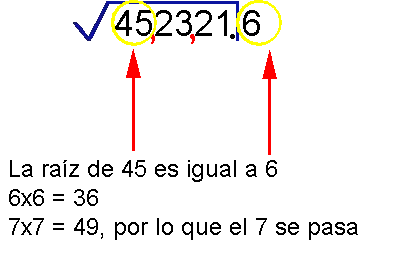
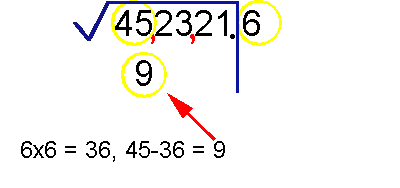
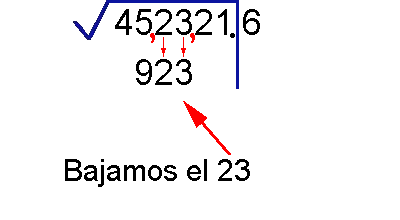
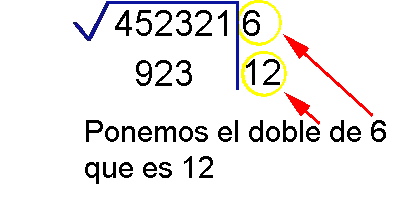
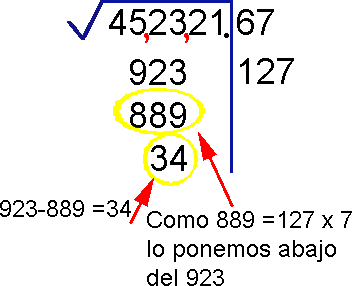
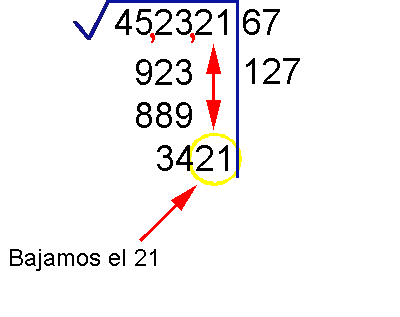
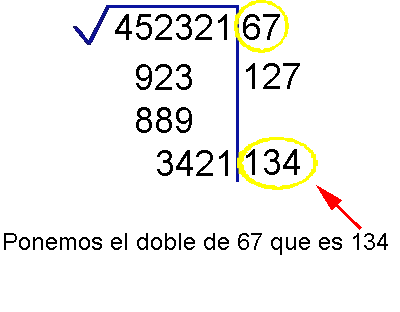
¿Te gustó?

¿Lo entendiste?

Aquí tienes más ejercicios resueltos

valor absoluto

Valor absoluto

En matemática, el valor absoluto o módulo¹ de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.

El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.

Valor absoluto de un número complejo[editar]

El valor absoluto de un número complejo

z\,

es la distancia

r\,

desde

z\,

al origen. Aquí vemos que

z\,

y suconjugado

\bar{z}\,

tienen el mismo valor absoluto.

Como los números complejos no conforman un conjunto ordenado en el sentido de los reales, la generalización del concepto no es directa, sino que requiere de la siguiente identidad, que proporciona una definición alternativa y equivalente para el valor absoluto:

|a| = \sqrt{a^2}

De esta manera, dado cualquier número complejo de la forma

z = x + iy\,

con x e y números reales, el valor absoluto o módulo de z está definido formalmente por:

|z| = \sqrt{x^2 + y^2}

Como los números complejos son una generalización de los números reales, es lógico que podamos representar a estos últimos también de esta forma:

|x + i0| = \sqrt{x^2 + 0^2} = \sqrt{x^2} = |x|

De modo similar a la interpretación geométrica del valor absoluto para los números reales, se desprende del Teorema de Pitágoras que el valor absoluto de un número complejo corresponde a la distancia en el plano complejo de ese número hasta elorigen, y más en general, que el valor absoluto de la diferencia de dos números complejos es igual a la distancia entre ellos.

ejemplos

funcion cuadratica

http://es.wikipedia.org/wiki/Funci%C3%B3n_cuadr%C3%A1tica

Función cuadrática

En matemáticas, una función cuadrática o función de segundo gradoes una función polinómica definida por:

$y = ax^2 + bx + c \,$

con $a \ne 0$ .¹

Las gráficas de estas funciones corresponden a parábolas verticales (eje de simetría paralelo al eje de las ordenadas), con la particularidad de que cuando a>0, el vértice de la parábola se encuentra en la parte inferior de la misma, siendo un mínimo (es decir, la parábola se abre "hacia arriba"), y cuando a<0 el vértice se encuentra en la parte superior, siendo un máximo (es decir, la parábola se abre "hacia abajo").

El estudio de las funciones cuadráticas tiene numerosas aplicaciones en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.

La función derivada de una función cuadrática es una función lineal y su integral indefinida es una familia de funciones cúbicas.